美国标准普尔500回报率中的黑天鹅问题——厚尾和非正态分布

张聚宝  波士顿学院商学院兼职教授

当我们讨论压力测试时，往往更关注小概率的风险，即尾部风险。马科维茨关于投资组合优化的博士论文发表后，奠定了现代金融投资管理的基础，也为他后来赢得了诺贝尔经济学奖。他的许多理论现在还被广泛应用，特别是其中一个很重要的假设：正态分布。在学界，正态分布已是一个老生常谈的问题，但大家都知道很多情况都是非正态分布，可是工业界主要还在沿用正态分布假设进行风险管理。这篇文章从美国标准普尔 500历史数据入手，探讨非正态分布问题，进一步思考对于风险管理和压力测试的影响。对 2007 至 2009 年的金融风暴或者 2020 年疫情这样的情况，或许有所帮助。

首先，什么是金融风险？ 风险没有一个统一的定义，不同的人可能有不同的定义，但总体来说更倾向于理解为对于潜在损失的计量。习近平总书记2019 年的讲话说到，既要高度警惕黑天鹅事件，也要防范灰犀牛事件。尽管总书记并不局限于金融风险，但这些概念在金融风险中是至关重要的。实际经验中，会有不同种类的风险考虑。比如在基金管理中，大家更多的会关注每天的、连续的变化，但实际上这种风险并不是很大。如果问一个基金经理或首席风险官，在他们心目中，日常风险是什么？一般回答都是风险敞口、久期等，而这些都是相对来说可测的。如果问令他们夜不能寐的风险是什么，那很可能就是一些小概率事件，比如黑天鹅或者灰犀牛事件。

金 融同很多基础科学相比，它更像是一种实践性科学，业界与学界实际上差别挺大。学界的一些研究是非常有益的，比如马科维茨的投资理论，Black-Scholes 期权定价模型等，但也有一些是超前甚至脱节的。（非）正态分布在学界听起来是一个基本概念，但在实践中大部分的基金经理对正态分布的理解是非常浅显的。一旦讲到非正态分布、厚尾等，很多人就更难以接受，而背后的数学变得复杂很多，更难解释和被接受。因此如何将实践与理论相结合，在金融这个学科里是很有意义的。美国一个著名的棒球队员 / 教练 Yogi Berra 说过： In theory there is no difference between theory and practice. In practice there is 。这句话对金融很适用。

标准普尔的回报率，很大程度取决于宏观经济。 图1是美国过去 15 年的美联储短期利率。众所周知，美联储有两个主要任务：控制通货膨胀和刺激经济（降低失业率）。可以看出，从 2004 年到 2020 年三、四月份，美联储一直没怎么消停，在 2007 至 2009 年金融风暴之前几年，他们不断地提升短期利率，目的是把经济就像爬山一样放缓。金融风暴发生以后，又急剧地降低利率，在降到接近零利率的时候，开始进行持续的量化宽松操作。 2016 年开始反转，慢慢地提高利率，直到 2019 年年底出现问题而停止，随着 2020 年 3 月份疫情的到来，迅速降到零利率，同时提供无上限的量化宽松。

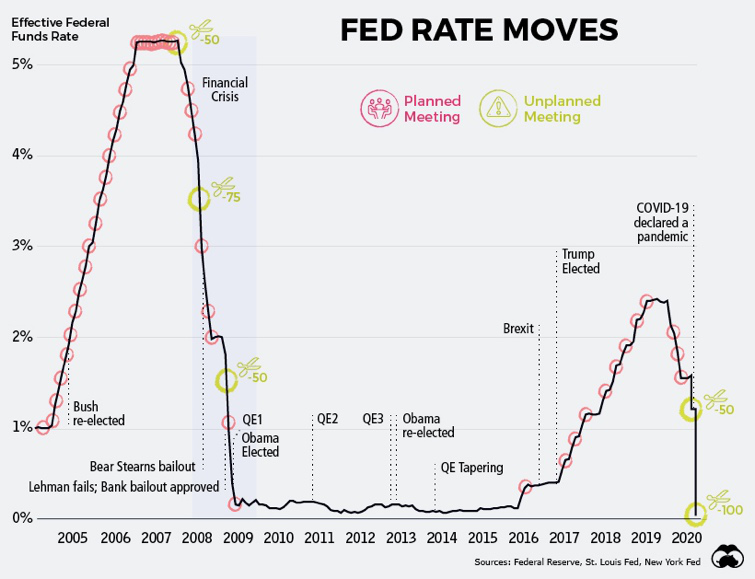
图1 美联储利率调整

股市与宏观经济息息相关。图2左图是过去 50 年标准普尔每一天的收盘价格，用于本文的分析。右图是 2020 年这一段短时间的放大观察，其中可以通过对 2020 年 3 月份的重点分析来看其中的非正态分布问题。

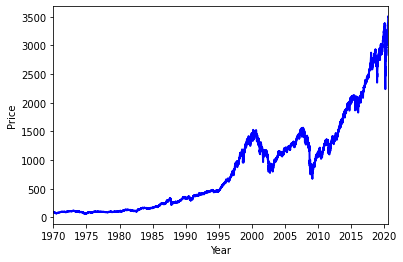
图2 1970-2020年标准普尔收盘价格

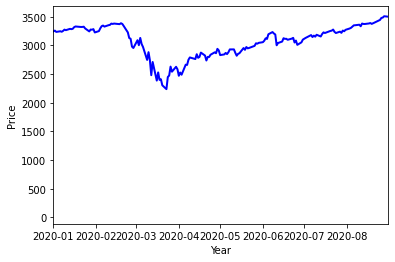
图3 2020年上半年标准普尔收盘价格

关于非正态分布与厚尾，它们实际上是同一概念。所谓的厚尾，它是相对于正态分布而言的，位于两端小概率分布中，如果异常正负（比如每天升跌超过3% 或者 4% ）概率大于正态分布，则把这种现象称为肥尾，也就是一种非正态分布，它的最重要体现是小概率事件出现几率大大增加。压力测试和风险管理特别重视肥尾的出现，因为它可能导致许多人失去工作，也可能让很多人损失多年积累的财产。

为了验证这种非正态分布，使用2020年疫情下（ 2 月至 6 月）美国标准普尔 500 的数据，计算每天的回报率，然后把其中超过 4% 上升或损失的挑选出来。根据美国 50 年标准普尔的分布，大约来说每一天它的标准方差，基本上都在 1.05% 左右（简单估算可以用 1% ）。如果假定满足正态分布，就可以用一个正态函数来计算每一个回报率的累积概率，然后转换成多少年才可能出现一次（假定一年 252 个交易日）。结果列在图 4 。

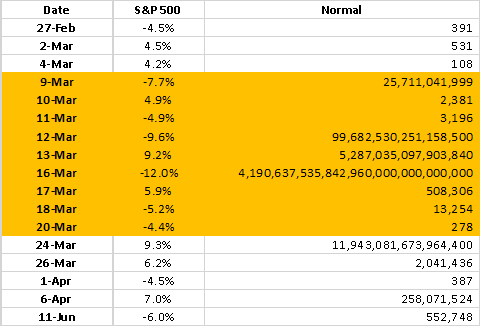
图4 正态分布下S&P500回报率的出现概率

以2月 27 日为例，这一天 S&P 下跌了 4.5% ，在一个正态分布中其累积概率大约为 1x10^-5 ，或者说每98532个交易日出现一次，也就是大约 391 年一次。可以看到，在短短的 4 个月之内，有一二十天出现了在正态假设下的小概率事件。按照正态分布，我们一生都难以看到一次这么大回报率的出现，但短短四个月却多次出现，特别是从 3 月 9 日到 3 月 20 日几乎每个交易日都是这种近乎不可能的波动。直观的解释，就是正态分布应该被推翻。再来看一个极端的例子，黑色礼拜一（ 1987 年 10 月 19 日），这一天 S&P 下跌 20.4% 。用正态分布来算，它出现的概率大概是 10 ⁸² 年，远远超过宇宙的生命，是一种几乎不可能出现的现象。

关于厚尾如何确定，还可以用QQ Plot来进行观察，如图 5 所示，其中红线是理论分布，而蓝色的点是每一天的实际回报率。可以看出，每天上升 1% 和下跌 1% 之间，基本能满足正态分布。但一旦到了 2% 之外，正态分布将远远低估出现的概率。作为比较，可以使用 Student t 分布，代入数据进行模拟，结果会接近很多。简单地说， Student t 分布从模式结果和相对简单，到风险管理应用，都比正态分布优越很多。

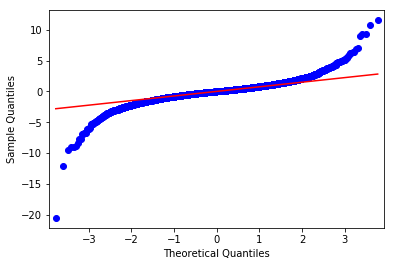
图5 正态分布下的QQ Plot

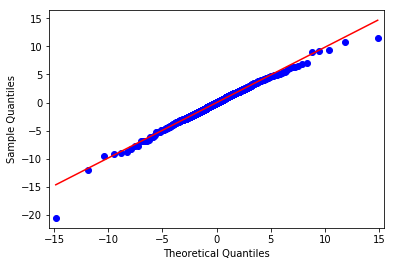
图6 Student t分布下的QQ Plot

利用Student t分布再重新计算 2020 年疫情出现的概率，并与之前正态分布的结果作比较。可以发现，如果下跌 4.5% ，在正态分布中是 400 年出现一次， Student t 分布中则每年都可能出现一次，尽管概率还是很小，但要比正态分布的高了 400 倍！再看大波动的 3 月 16 日，正态分布中每 10²⁷ 年的概率，而在Student t分布中是 34 年出现一次，这是好多亿倍的差别。

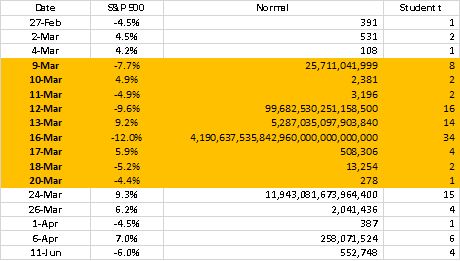
图7 Student t分布下S&P500回报率的出现概率

将Student t分布与正态分布相比，对于小概率事件，比方说在一天内出现 4% 、 5% 的回报率，它的概率会差几百几千倍；如果是 7.7% ，则会相差千万百万级的倍数。由此可知，越是小概率事件，两者的结果相差倍数越高。一个相关的问题是波动率随时间变化，如果用 GARCH 模型，计算得到的短期波动率会起伏，在 2020 年 3 月份会有明显提升，用这个波动率来计算异常回报率概率，会有一些回落，更接近现实。当黑色礼拜一用 Student t 分布来模拟时，出现的概率会变成 188 年。如果再引入变动的波动率，很有可能变成几十年，这种可能性是存在的，而正态分布下比宇宙生命还长 10 ⁸² 年的概率即便有波动率修正也是极不现实。

正态分布在工业界是一个常规假设，这对于压力测试和风险管理带来很大挑战。非正态分布（厚尾）的本质，是越往两端走，正态分布会越严重低估真正可能出现的概率，特别是黑天鹅事件，正态分布会给人盲目乐观而导致应对不足。

来源：2020（第十六届）中国金融风险经理年度总论坛（11月）