一、信用风险研究存在的问题

       信用风险是所有风险种类中最为常见的风险。以银行为例，其几万亿资产面临的最大风险就是信用风险。目前，在学术领域，对于信用风险的研究并不是很多，研究方法也主要是从市场风险借鉴而来。但在实践中，信用风险存在的问题却是不容忽视。第一，数据不透明。与其他风险不同，各家银行很少提供信用风险的相关数据，因此很难进行详细研究。第二，标准不同。不同银行的数据缺乏统一性，即使是同一家银行不同人所做出的判断也存在差异，因此缺乏标准化概念。第三，过多的人为判断。从实践角度来说，信用风险很大程度取决于人的判断，即使是同一家银行同一个部门所做出的判断也可能存在分歧。第四，信用评级来源多样。一种是由政府指定的专门评级机构，如穆迪、标普和惠誉；一种是银行自身，每家银行有自己的评级标准和方法；此外，学术界的专家学者也存在很多不同的研究方法，从而产生不同的评级结果。以上因素给信用风险的研究和理解造成了一定的困难。

二、公司信用评级

       信用评级可以分成两大类，一类是对公司的评级，一类是对个人的评级。个人评级，又称为信用打分，主要是对普通消费者进行评级。与消费者评级有大量的数据不同，由于公司破产特别是同类公司破产的情况相对较少，获取公司违约率是非常困难的，因此对公司评级难度很大。

       例如穆迪公司给出的B评级的历史违约率。在2001年，由于金融危机及其所造成的经济衰退，B等级的历史违约率为9.8%。而到2007年，违约率为0；在2009年又达到一个高峰，之后又再次降下来。因此，从违约率角度来看，评级公司所做的信用评级并没有一致性。但事实上，这些评级又是评级机构的专家采用同样的评级办法和评级标准通过研究公司的财务状况、运作模式、所处行业等计算出的结果。而这种结果似乎是无法解释的。不仅是评级公司，所有银行也面临同样的问题。

      在学术界，Merton将期权定价理论应用到公司违约率的计算上。他发现公司的资产价值与股价之间实质上是期权关系，因此可以计算出违约价值。因此，公司违约本身可以看做是一种权利，如果价值高的话，公司会考虑违约。任何理论都会存在一定的问题，此外对于已经存在的各家银行的评级，如何进行比较和转换，需要制定一定的标准，但这种标准又是实时在变化需要不断调整的。

三、信用的数学定义

       鉴于关于信用风险的诸多问题，我们首先要讨论一下银行、金融机构乃至专家学者所讨论的“信用”到底是怎么回事。这是理论研究的第一个出发点。第二个出发点在于，如果不同主体所讲的信用不同，有没有什么办法进行说明。我认为要将上述问题讲清楚，首先需要有一个严格的数学定义。目前穆迪等评级机构对信用风险的衡量都是用语言进行的定性描述。此外，这个定义最好能够将专业评级机构、银行和专家学者的定义都包含进去。以此为基础，来研究上述问题能否完全得到解决。

       关于违约，每家银行都有其不同的定义，而违约的百分比就是违约率。我们假定一家公司在一定时间区间内违约的概率是百分百，那么公司的预期寿命就可以替代违约率来描述公司信用。在这种逻辑下，如果一家公司只能存活100年，那么其违约率就是1%；如果只能存活50年，那么违约率就是2%。尽管如此，现实中还是存在一些寿命解释不了的问题。因此，除了寿命之外，还需要信用相关的另一重要要素——经济资本。经济资本与评级有密切关系，可以与预期寿命共同定义信用。

       上式中，分母表示预期寿命，分子是将经济资本及其他要素结合得到一起得到的。对公式可以做如下解释：一个人或一个公司的寿命是存在长短的，这大概可以决定其信用好坏，但预期寿命又不能起到完全决定作用，还有一些辅助力量，正如人一生中也会面临各种可能对生命造成伤害的因素，因此寿命损害的速度也是信用的组成部分。因此，信用被两个因素所定义，一是寿命，二是寿命的损耗率。

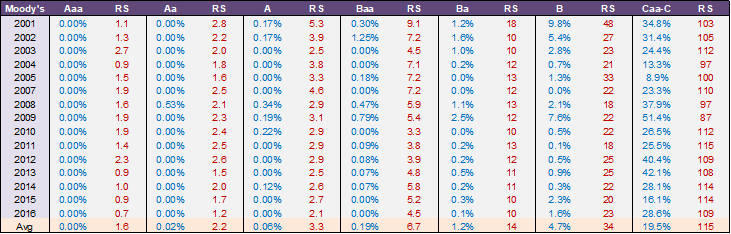
      那么，这个公式又是如何应用到所有的案例中呢？Q值表示一个取决于评级体系的常数。穆迪的Q值为0.746，标普为0.626，各家银行大约在0.5至1之间。用Merton的公式计算出的Q值为1。由此可以看出，不同单位对于信用的定义确实存在差别，在数学上可以将其详细区分出来。其差别实际就在于一个常数Q，这个常数表示损耗率与寿命的比率，即如果一个人寿命缩短了一倍，但损耗率也降低了一倍，其信用水平是不变的，而这一公式就可以将所有的评级系统都纳入其中。下图展示了实际的评级结果。

       图中每个格子都表示了用公式计算出的不同的违约率。黑色表示最糟糕的3C评级，绿色表示的是最好的3A评级，每一个点表示不同的年份。可以发现，黑色点近乎排成了一条直线，但不同年份的违约率是不同的；直线斜率等于0.75，与其评级具有一致性。不同违约率之所以在同一条直线上，是因为它将长期的利率与短期利率进行了交换。当违约率增大时，短期损失就会变大，但是相对而言长期利率就不会损失那么多。因此，基本上线上的每一个点，都可以用很精确的数学公式告诉我们它做了一个什么样的交换，也就是可以翻译成我们的刚才讲的经济资本的语言。

       众所周知，银行有两个非常重要的指标，一个叫储备金，备付的是下一年的损失；另一个是资本，以防止银行破产。这里的交换是指当近期损失变大时，未来损失会变小，换言之，是在资本跟短期储备金之间的一个交换。正因为这种交换使得在违约率每年不同的情况下评级一致。因为违约率只是对应的近期利率，而没有考虑长期利率。

       有了数学公式，就可以用公式来定义等级，且数值为连续的（表格红字所示）。这些数值呈现出一个特点，即在2010年到2016年间，每个级别的数字基本一致。这意味着，通过数学公司定义出的等级是穿越周期的，即不存在在不同年的同一家公司有不同等级，因此评级具有一致性。而如果同一家公司，在其本质上没有发生变化的情况下在不同年份不一样，这个评级将没有意义。这一点是非常重要的。

       用来计算违约率的公式如下所示，这个公式并不是统计的经验公式，而是用数学推导出来的。其计算结果与穆迪的结果基本一致，可能存在万分之几的误差。所以这个公式告诉我们很多事情，包括信用评级有两个组成部分，第一个是PD，也就是违约概率；第二个叫λ，它决定了经济资本。

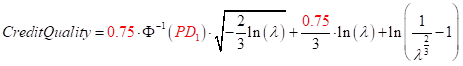
       在研究中，我经常得到很多令人吃惊但又非常有意思的结果，然后再回头进行验证，又会有新的发现。这使我对信用有更为多样而深刻的理解。例如，Merton将股市市价与资产波动性和资产市值相联系，假定通过观察股市就可以推导出公司在市场真正的价值。而我所推导的公式可以在不知道股市的情况下就可以计算出其资产的价值。这个公式将信用、违约以及其他要素联系在一起，当对λ用不同的观点进行解释的时候，你会得到意想不到的结果。