新资本协议下的资本分配方法实践探讨

陈公越 凯美瑞德高级顾问 杭州巨慧达科技总裁

一、为什么需要资本分配？

随着巴塞尔协议Ⅲ在国内银行开展实施，从需求角度也慢慢提出来了资本分配方法这个议题，即除了计算市场风险加权资本、信用风险加权资本以外，会提出怎样做资本的分配。

资本分配这个议题确实能回答商业逻辑中的一些重要问题：我们最大的风险是什么？风险的分散性来源在哪里？比方确实值得去做这一笔交易，会给组合风险带来正向分散呢还是负向分散？承担风险的回报和组合整体的回报有什么关系？当然可以计算风险回报指标，或风险贡献度，或者怎么样基于指标进行风险定价。

二、跨资产组合的资本分配

在欧美的学术中，跨资产组合的资本分配——欧拉分配算法（Euler allocation）是得到普遍认可的，从理论上提供了有效的途径，有些商业产品开始提供这样的算法。这个算法具有优良的特性，相对易于计算，解释性比较直观。

三、FRTB市场风险监管资本标准法

以市场风险的监管资本作为例子，原来计算方法和当前的计算方法差异在什么地方？原来巴塞尔协议Ⅱ的标准法，可以归纳为一种线性的资本需求计算方法，但巴塞尔协议Ⅲ的资本需求是基于每一笔交易的头寸敏感度指标进行计算，分别包括对风险因子Delta资本的计算、包括波动率的vega资本要求计算、针对非线性情况下的资本需求，此外还考虑违约资本，包括债券、股权和资产证券类违约资本的计算。对复杂衍生品而言，会针对一些没有覆盖的风险进行计算，比如剩余风险资本要求。所以即使有标准法，很难用一个线性的模型描述资本的计算结果。

FRTB的核心要求：整个资本计算不存在一个线性的关系，比方说它有各种判断要求，在风险层面进行汇总，然后从大类风险又分别进行汇总。另外，在违约风险计提下面，又存在风险投资净值抵消金额折扣的风险对冲比例。剩余资本的计算比较直接，按照一个线性的头寸敞口来进行计算。

四、问题和思路

如果给出了一个风险指标，假设我们直接用FRTB资本计算，或者从FRTB资本衍生出经济资本的计算指标，组合经济资本不等于每一个交易头寸下面的风险的计算总和，这从理论上称为典型的非sub-additive属性。

风险指标就不可以直接用于线性的分配方式，欧拉分配的思路是找到一组变量，针对每一个交易头寸都要设置相应的参数，使其乘积之和等于组合损益。欧拉分配原理如下：

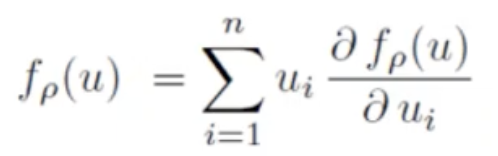
如果函数具有解析解，我们可以试图采用解析解方法获得算法，通过偏微分这个方程的分解推导出来，国外从2010年左右开始探讨这个问题。比方说对有封闭解的，用一个偏微分的标准差计算，从数学上是可以推导出这解析解，但是实践上很难找到一种理想方式。

比如市场风险的标准法也好，或者用内模法、历史模型法或者蒙特卡罗的模拟法，本身就有一个解析解去推导，没有解析解的方法怎么办？一般就只能通过模拟数据样本的方法去做，基本思路如下：

大多数情况下，如果没有解析解，可以采用模拟的或者历史的数据样本进行估算。如果数据量足够大，可以基于大数定理，采用核密度方法进行估算。

同样，针对信用风险，也是需要一定的调整的。从模拟法角度讲，信用风险的挑战确实比较大，从数据角度讲，市场风险的模拟是比较完善的，可以用历史模拟，如果交易是确实信息，可以直接从历史损益进行数据采集。即使没有市场交易的历史信息，可以对风险因子进行模拟，对损益用蒙特卡洛模拟方法，模拟出一组历史损益的模拟样本，可以直接采用核密度方法。

对于传统的方法，很多银行就直接把监管资本作为调整项，可能就直接在资金资本分配里用，但是对于市场风险，这个方法肯定是有问题的。所以，欧美很多银行开始采用欧拉方法。那么，国内的银行是不是应该采用这个方法？这是一个可以探讨的问题。

演讲稿整理：俞甜甜

责任编辑：傅泽天

来源：TGES 2021（第十七届）中国金融风险经理年度总论坛：资本、风险偏好和限额管理（12月）