沈雁 衍生品交易和风险管理国际资深专家
任何一个期权市场的隐含波动率不可能是一条直线,它一定会出现倾斜或者是微笑的形状,例如,利率衍生品的波动率是倾斜的,即利率越低,波形率越高;大部分股票也会出现股价越低波动率越高的情况;对于汇率以及商品的衍生品,它们的波动率有时候会右倾,有时左倾。大家所熟知的收益率呈对数正态分布是一个非常大胆的假设,特别是在奇异型期权方面。对于奇异型期权,它的payoff不是一个连续的函数,这会导致奇异型期权的风险指标有比较大的敏感性。基于此,我们提出一个具有波动率倾斜或微笑的模型族群,然后我们首先发现该模型族群具有期权对称性,期权对称性是指,在组合中存在一点的价值不会随波动率的倾斜、微笑而改变。得到了期权对称性性质后,我们只需要管理一组常规欧式期权就能够起到管理奇异型期权的市场风险的作用,同时也可以通过复制得到在具有波动率微笑的市场中的奇异期权的定价。在实践上,我们提供了一个非常简便和可操作性的复杂型期权的定价、风险分解和对冲管理手段,这是我们最主要的贡献。
随机微分方程为一个平移型对数正态随机过程: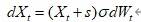
假设转移密度函数为: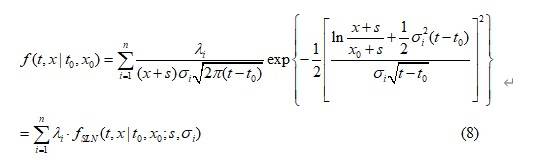
其中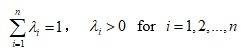
 。参数
。参数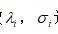 ,还有各子密度函数共同使用的s为模型使用者需要确定的。根据上述,该模型族应有以下性质:
,还有各子密度函数共同使用的s为模型使用者需要确定的。根据上述,该模型族应有以下性质:
对于任意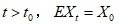 ,满足鞅的条件。
,满足鞅的条件。
如果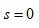 ,多个对数正态模型的密度混合。
,多个对数正态模型的密度混合。
如果 ,多个正态或者高斯模型的混合。
,多个正态或者高斯模型的混合。
如果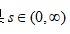 ,多个平移型密度函数的混合。
,多个平移型密度函数的混合。
在波动率交易中,我们将持有具有同一到期日,但行权价格和多空方向不同的期权的组合称为风险翻转。风险翻转是对冲波动性倾斜最基本、最常用的交易策略。因为很多复杂的风险组合可以分解为一个或多个风险翻转结构来对冲其敞口。然而下面讨论的对称性更加强调了风险翻转结构的重要性。典型的例子如下:进入T到期的认购期权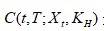
 多头,同时进入
多头,同时进入 份
份 到期的认沽期权
到期的认沽期权
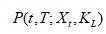 空头,并且
空头,并且
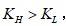 ,这个组合可以写为:
,这个组合可以写为: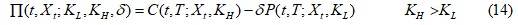
一般情况下,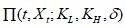 随着市场变化而变化,然而我们感兴趣的是:如果我们选定了某描述期权市场的模型,那么是否存在某一个特殊的标的价格B,在任何时刻
随着市场变化而变化,然而我们感兴趣的是:如果我们选定了某描述期权市场的模型,那么是否存在某一个特殊的标的价格B,在任何时刻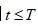
 ,不管
,不管 在这个过程中交易到什么水平,只要任何时候
在这个过程中交易到什么水平,只要任何时候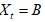
 ,我们可以使
,我们可以使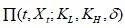 =0,如果B存在,那么则称该模型具有期权对称性。
=0,如果B存在,那么则称该模型具有期权对称性。
我们证明了以下定理:
定理1(平移型模型存在期权对称性):给定模型以及参数s,对于期权组合
 。存在一个唯一的价格B满足
。存在一个唯一的价格B满足
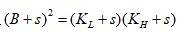 。
。
如果选定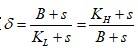
 ,那么对于任意的
,那么对于任意的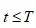
 ,以及任意的
,以及任意的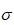
 ,只要
,只要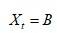
 ,那么
,那么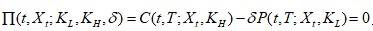 有
有 成立。
成立。
定理2(混合平移密度函数模型族存在期权对称性)。给定模型(8)及其参数s,对于期权组合(14),存在一个唯一的价格B满足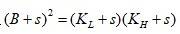 。
。
若选定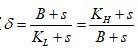
 ,那么对于
,那么对于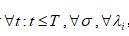 ,
, 只要
只要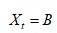
 ,那么有下
,那么有下
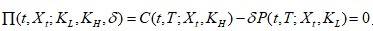 成立。
成立。
在上述定理成立的条件下,我们可以得到以下期权对冲方法:
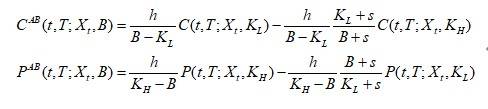
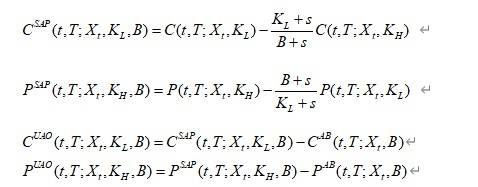
定义1(ABS模型),在(8)中选择n=3,并引入两个非负参数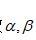
 。令:
。令: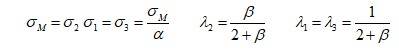
我们可以调节来控制波动率微笑程度。
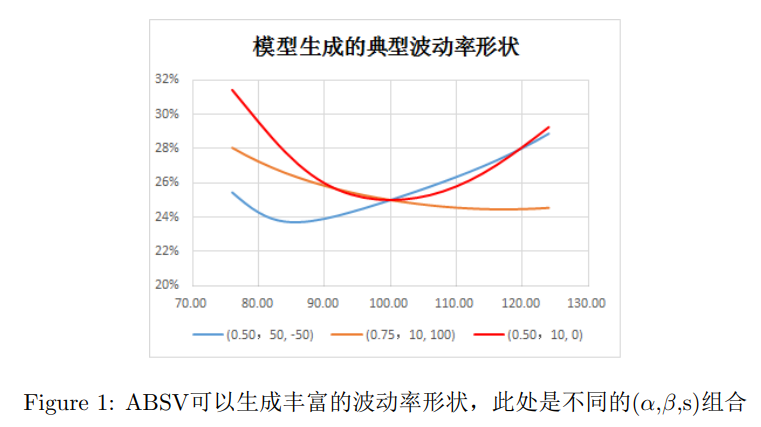
图 1 ABS模型生成的波动率形状示例
ABS可以产生多样的波动率微笑形状。如图1所示,我们设在100处于平值,国内铜的衍生品的波动率微笑与图中红色的线相似,现在一些化工产品的波动率呈现出如黄线的倾斜。
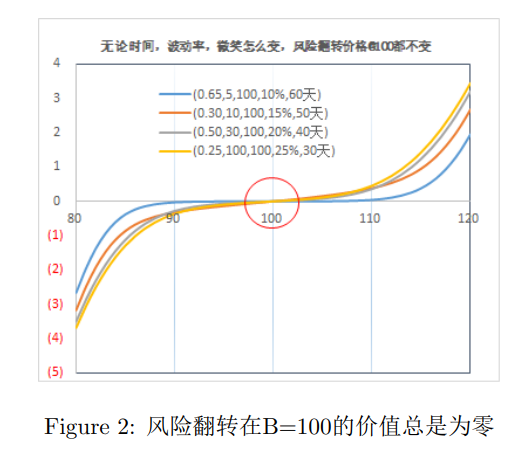
图 2 风险翻转在B=100处恒为0
在不同的波动率的形状以及不同的时间参数下,总是存在一点,其风险翻转为0,静态复制的整体原理即在此。上文中证明了任何的奇异型期权,都可分解成不同的风险翻转结构的组合,如果我们找到风险翻转结构的对称点,那么所有期权基本上可以被复制。在实际中,这可以大大简化奇异型期权风险管理的过程。
责任编辑:奉琳竣
来源:2020(第十六届)中国金融风险经理年度总论坛